torch笔记六 | 搭建一个简单的与运算神经网络
本文共 4649 字,大约阅读时间需要 15 分钟。
1.任务目标
“与”运算,即and运算:输入两个数字,如果两数均为真值1,输出才为1,其他情况均输出0。使用pytorch搭建了一个简单的与运算神经网络,熟悉一下搭建网络的大体流程。
2.设计步骤
(1)导入需要的库
第一个导入torch包。导入numpy包,创建矩阵作为输入,并用np代替numpy,减少字母方便接下来编写代码。最后导入torch中的nn,并用nn替代。nn是神经网络(neural network)的缩写,是专门用来搭建网络的一个包。
# 1.导入需要的库 import torch #导入torch包 import numpy as np # 用np代替numpy import torch.nn as nn # 用nn代替torch包里的nn
(2)构建输入集和理想输出集
使用numpy创建矩阵作为输入,包含(0,0),(0,1),(1,0),(1,1)的4种情况。并用同样的方法构建与输入对应的理想输出集0,0,0,1。
注意:一定要把numpy创建的数据转换成pytorch框架需要的tensor变量。在深度学习里,Tensor(张量)实际上就是一个多维数组,Tensor的目的是能够创造更高维度的矩阵、向量。
# 2.构建输入集和理想输出集 # 构建输入集 x = np.mat('0 0;' '0 1;' '1 0;' '1 1') # mat可以从字符串或列表中生成数组x = torch.tensor(x).float() # 把输入转换成浮点型的tensor变量 # 构建对应的理想输出集 y = np.mat('0;' '0;' '0;' '1') # 创建与输入集对应的理想输出集 y = torch.tensor(y).float() # 把理想输出转换成浮点型的tensor变量 (3)搭建网络
使用nn包中的Sequential函数搭建网络。
输入层:要输入两个数字,所以设置2个输入节点。问题比较简单,隐藏层设置8个节点就够啦。 Linear(2,8)是生成具有2个输入节点,8个输出节点的输入层。 隐藏层1:ReLU()就是一个激活函数层,线性整流函数( ReLU)通常意义下指代数学中的斜坡函数,即 f(x)=max(0,x) 。 隐藏层2:Linear(8, 1)是有8个输入节点,1个输出节点的线性层,回收数据便于输出的作用。 输出层:Sigmoid函数是一个常见的S型函数,也称为S型生长曲线,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。
# 3.搭建网络 # 使用nn包中的Sequential函数搭建网络 my_Net = nn.Sequential(nn.Linear(2, 8), # 输入层 nn.ReLU(), # 激活函数层 nn.Linear(8, 1), # 线性 nn.Sigmoid()) # 输出层 print(myNet)
(4)设置优化器
传入网络参数(myNet.paramets)和学习率(lr),采用SGD方法训练优化。
# 4.设置优化器# 传入网络参数和学习率,采用SGD方法训练 optimzer = torch.optim.SGD(myNet.parameters(), lr=0.05)
(5)设置代价函数
# 5.设置代价函数# 使用MSE均方误差代价函数,设置代价函数 loss_func = nn.MSELoss()
(6)训练网络
设置一个3000次的循环,迭代训练我们搭建的网络。
首先将数据x扔给网络my_Net得到计算结果,将计算结果与理想输出做比较求出误差,清除上一次计算得到的梯度,让误差反向传播,启动我们设计的优化器,不断优化更新神经元的参数,不断降低梯度,使得误差最小。# 6.训练网络 # 设置一个3000次的循环 for epoch in range(3000): out = my_Net(x) loss = loss_func(out, y) # 计算误差 optimzer.zero_grad() # 清除上一次的梯度 loss.backward() # 让误差反向传播 optimzer.step() # 让优化器工作
(7)测试结果
将输入和实际输出显示在屏幕。.data的意思就是只输出tensor中的数据,并不显示tensor中的其它参数。
print("input is\n %s" % x) print("output is\n %s" % myNet(x).data) 3.运行结果
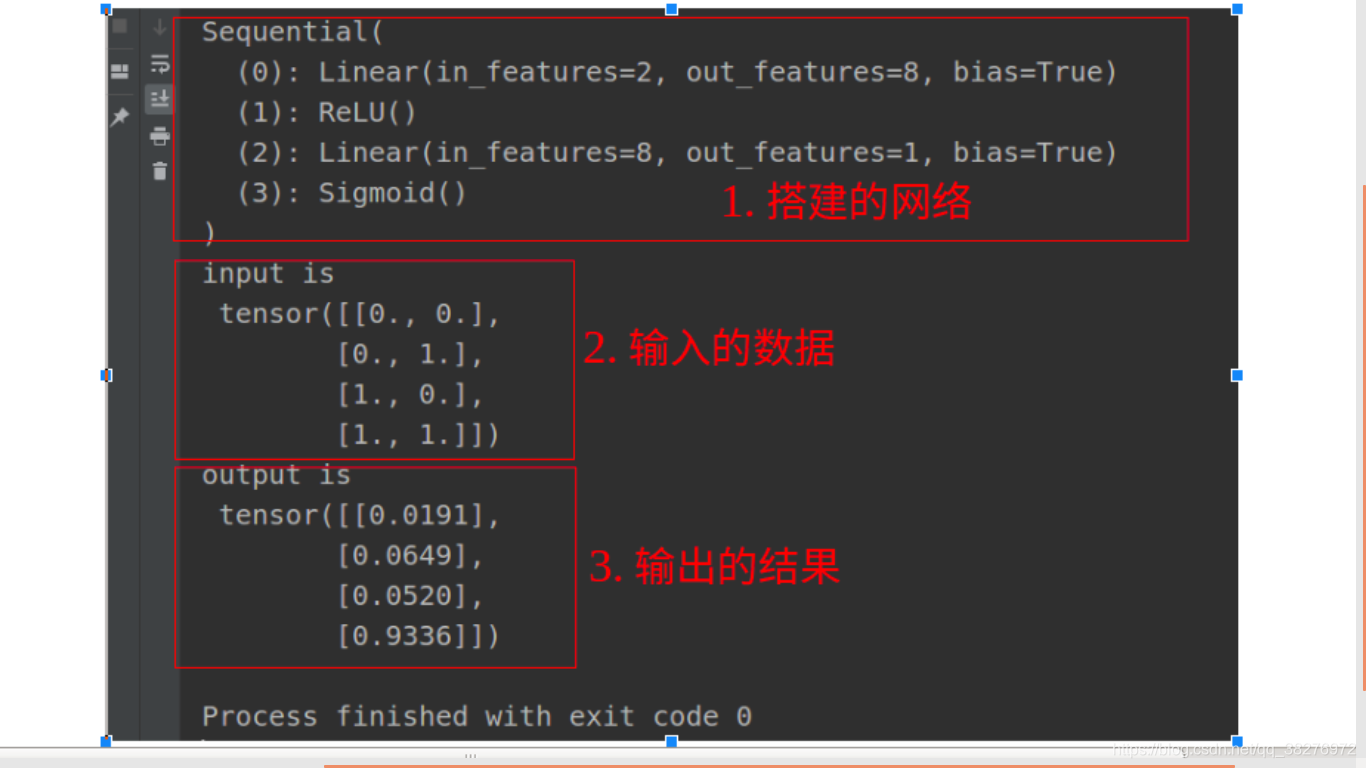 由上图运行结果可以看出,输出的结果与理想的输出基本一致,训练的网络具有不错的效果。
由上图运行结果可以看出,输出的结果与理想的输出基本一致,训练的网络具有不错的效果。
完整代码附下:
# 1.导入需要的库 import torch #引入torch包 import numpy as np # 用np代替numpy import torch.nn as nn # 用nn代替torch包里的nn # 2.构建输入集和理想输出集 # 构建输入集 x = np.mat('0 0;' '0 1;' '1 0;' '1 1') x = torch.tensor(x).float() # 把输入转换成浮 # 构建对应的理想输出集 y = np.mat('0;' '0;' '0;' '1') # 创建与输入y = torch.tensor(y).float() # 把理想输出 # 3.搭建网络 # 使用nn包中的Sequential函数搭建网络 myNet = nn.Sequential(nn.Linear(2, 8), nn.ReLU(), nn.Linear(8, 1), nn.Sigmoid()) print(myNet) # 4.设置优化器 # 传入网络参数和学习率,采用SGD方法训练 optimzer = torch.optim.SGD(myNet.parameters(), lr=0.05) # 使用MSE均方误差代价函数,设置代价函数 loss_func = nn.MSELoss() # 5.训练网络 # 设置一个3000次的循环 for epoch in range(3000): out = myNet(x) loss = loss_func(out, y) # 计算误差 optimzer.zero_grad() # 清除上一次的梯度 loss.backward() # 让误差反向传播 optimzer.step() # 让优化器工作 # 6.测试 print("input is\n %s" % x) print("output is\n %s" % myNet(x).data) 转载地址:http://yznq.baihongyu.com/
你可能感兴趣的文章
Netty源码—6.ByteBuf原理一
查看>>
Netty源码—6.ByteBuf原理二
查看>>
Netty源码—7.ByteBuf原理三
查看>>
Netty源码—7.ByteBuf原理四
查看>>
Netty源码—8.编解码原理一
查看>>
Netty源码—8.编解码原理二
查看>>
Netty源码解读
查看>>
Netty的Socket编程详解-搭建服务端与客户端并进行数据传输
查看>>
Netty相关
查看>>
Netty简介
查看>>
Netty速成:基础+入门+中级+高级+源码架构+行业应用
查看>>
Netty遇到TCP发送缓冲区满了 写半包操作该如何处理
查看>>
Netty:ChannelPipeline和ChannelHandler为什么会鬼混在一起?
查看>>
Netty:原理架构解析
查看>>
Network Dissection:Quantifying Interpretability of Deep Visual Representations(深层视觉表征的量化解释)
查看>>
Network Sniffer and Connection Analyzer
查看>>
Network 灰鸽宝典【目录】
查看>>
NetworkX系列教程(11)-graph和其他数据格式转换
查看>>
Networkx读取军械调查-ITN综合传输网络?/读取GML文件
查看>>
network小学习
查看>>